What Is the Future of Individual Claims Reserving?

With the increased need for more accurate reserving models, taking advantage of the information embedded in individual claims data with appropriate claims development models is a promising alternative compared with the traditional aggregate loss development triangles (see "Basics of Loss Development Triangles"). Although not without implementation challenges, the future of individual claims reserving is enlarged by the innovative opportunities offered by these alternative individual reserving models.

The current reserving practice consists, in most cases, of using methods based on claim development triangles for point estimate projections as well as for capital requirement calculations. The triangles are organized by origin period (e.g., accident, underwriting) and development period. In recent decades, there has been great success with deterministic and stochastic unpaid claim reserving models based on triangles, such as those related to the popular chain ladder model or many others developed in the huge amount of related actuarial literature. Such models, especially in their stochastic form, have been used in order to measure and manage reserve risk for a variety of lines of business.

A Growing Awareness about Limitations of Traditional Methods

Traditional reserving methods have worked well in several circumstances in the past and will probably continue to do so in similar circumstances in the future. Today, however, the awareness of the insurance market about some possible limitations of traditional aggregate models to provide robust and realistic estimates in more variable contexts has reached a level that should be noted. Several potential limits of aggregate models based on triangles have indeed already been highlighted both from a practical and a theoretical point of view. These are mainly as follows.

• Over/under-estimation of the distribution when back-testing realized amounts with forecasts
• Huge estimation error for the latest development periods due to the lack of observed aggregate amounts
• Uncertainty about the ability of these models to properly capture the pattern of claim development, combined with the limited interpretive and predictive power of the accident and development period parameters

Overall, these limits are due to a loss of information when aggregating the original individual claim data details (e.g., time of occurrence, reporting delay, and time and amounts of payments, along with several other features) into basic origin and development blocks in the triangle. Recent developments in data collection, storage, and analysis techniques mean that a proper individual claim modeling is now accessible. On this basis, it has become crucial to implement more flexible models for operational uses (e.g., claims management, underwriting, reinsurance, etc.) to account for key effects, such as the following.

• Capturing the specific development patterns of claims, including their occurrence, reporting, and cash-flow features
• Taking into account possible changes in the product mix, the legal context, or the claims processing over time, to avoid potential biases in estimation and forecasting
• Performing an advanced risk assessment and monitoring (e.g., allowing for detection of trend changes)
• Implementing a separate and consistent treatment of incurred but not yet reported (IBNyR) claims
• Including the key claim characteristics (i.e., explanatory variables) to allow for claims heterogeneity and to take advantage of additional large data sets combined with big data and analytics technologies
• Gathering such features in a rigorous statistical framework allowing for goodness-of-fit analysis and model checking

In this context of rising demand for more accurate reserving approaches, a proper use of the information embedded in individual claims data combined with appropriate individual claim development models represent a promising future.

In comparison with aggregate approaches, few academic contributions investigated so far reveal the power of using the individual claims data for reserving purposes. As a consequence, few practical implementations have been performed in the insurance market. As noted in the report on worldwide nonlife reserving practices from the ASTIN Working Party on Non-Life Reserving (June 2016), there is "an increase in the need to move towards individual claims reserving and big data, to better link the reserving process with the pricing process and to be able to better value non-proportional reinsurance." The limited market spread of individual reserving approaches seems to be due to a lack of an innovation solution.

Moving Forward with Individual Claims Reserving

The individual claim point of view requires methodologies that are able to capture the detailed individual claim development. In this context, a "claim-based" modeling framework is needed, with a precise continuous time description of its life history made (see Figure 1) of the time at which the claim occurs, its reporting delay, the various payment amounts, and case reserve changes with their associated times, as well as the closing time. This modeling framework can be made flexible enough to take into account line-of-business specificities, such as recoveries and re-opening.

FIGURE 1

TYPICAL INDIVIDUAL CLAIMS PATHS

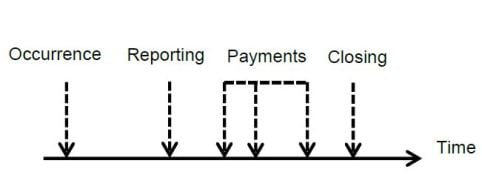
Continuous time modeling provides the most precise description of the portfolio time pattern. The mathematical tools at the core of the model specification lie in the family of continuous-time stochastic processes, known as marked point processes and multistate dynamics, which model all kinds of events related to claims history. It is interesting to note that stochastic models for unpaid claims reserving appeared at around the same time for both individual-based and triangle-based models. To our knowledge, Norberg (1993) and Hesselager (1994) are among the earliest papers that introduced a proper probabilistic setting for individual claims reserving, recently applied by Antonio and Plat (2014), whereas Mack (1993) proposed in his seminal paper a stochastic model underlying the triangle-based chain ladder technique. To date, we suspect that the greater success of the triangle-based models could be driven by their comparative ease of use and the lack of inexpensive computing power in the early days of these models.

In order to estimate the parameters for an individual claims model, a calibration procedure is performed based on likelihood maximization. Deriving the likelihood associated with the observed claims data set is a challenging step, as reported but not settled (RBNS) claims are only partly observed, while the so-called IBNyR claims are not observed at all. This introduces a sampling bias in the observation process that, from a statistical perspective, relates to censoring and truncation. As the individual claims model involves a reasonable number of parameters, often lower than in a triangle-based approach, and as the number of individual claims records is large in comparison, the likelihood maximization provides an efficient procedure that estimates the model parameters almost instantaneously.

As an added bonus, estimated parameters typically show natural explanatory powers (e.g., occurrence and reporting frequencies, average settlement delays, etc.), and separate payment distribution specifications can provide information on the building blocks of the overall claim development path. This way, the parameters allow for a detailed monitoring of key risk indicators that, with triangle-based approaches, are hidden in aggregate development factors and related volatilities.

As for forecasting, simulation procedures draw on stochastic paths of the future development of RBNS and IBNyR claims, as well as new claims that will occur in the future. The procedure allows the user to forecast future events in a very efficient way, whereas the patterns in the terms of claims arrival and time-to-event frequencies (as reporting and settlement delays) can be set as general as possible. Moreover, the simulation procedure can explicitly include anticipated changes in parameters (e.g., product mix, frequency trends, etc.), which helps avoid potential biases in the forecast. In its standard parameterization, the model also allows for closed-form formulas that provide overall unpaid claim estimates and the related confidence intervals in a straightforward way. The key components of the individual reserving methodology are illustrated in Figure 2.

FIGURE 2

INDIVIDUAL RESERVING METHODOLOGY

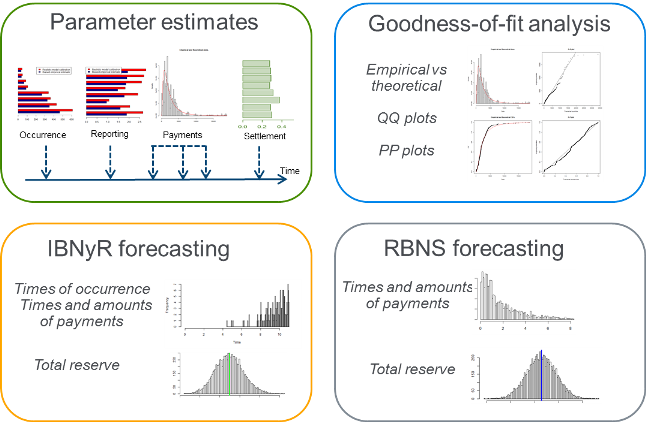
Step-by-Step Implementation of an Individual Reserving Process

Our team has developed individual claims models as a new way for actuaries to efficiently measure and manage risks. Individual claims reserving models are very promising. To meet the associated challenges, we designed an integrated reserving process covering data needs, modeling, and risk monitoring.

• Data collection and preparation: organize a standardized collection strategy focusing only on the claims data used by the individual claims model and perform the data transformation needed to feed the individual claims model.
• Model specification and calibration: specify the model components according to the lines of business to be addressed and the transformed data and estimate the parameters of the individual claims model using advanced optimization procedures combined with goodness-of-fit analysis.
• Model simulation and validation: forecast IBNyR and RBNS individual trajectories using efficient simulation algorithms and perform a model validation process based on back-testing procedures and comparisons with classical triangle-based models and benchmarks.
• Reserve risk dashboard: claims path parameters are visualized through an automated dashboard in order to periodically monitor the key indicators and leverage information to improve management actions.

This framework allows users to assess why things happened—that is, to identify underlying drivers that caused changes in aggregate payments. This can also lead to a reassessment of what will happen by improving forecasts and their associated uncertainty. Individual claims reserving models are now ready to deliver their full potential. Two building blocks will ensure a successful implementation: a strong modeling expertise combined with an optimized and rigorous data collection process. Even if the integration of individual claims reserving techniques within the landscape of reserving is neither immediate nor obvious, there is no doubt that these models will become a strong paradigm in which to evolve in the near future.

References

• Antonio, Katrien, and Richard Plat. "Micro-level stochastic loss reserving for general insurance." Scandinavian Actuarial Journal 7 (2014): 649–669.
• Hesselager, Ole. "A Markov model for loss reserving." ASTIN Bulletin 24 02 (1994): 183–193.
• Mack, Thomas. "Distribution-free calculation of the standard error of chain ladder reserve estimates." ASTIN Bulletin 23 02 (1993): 213–225.
• Norberg, Ragnar. "Prediction of outstanding liabilities in non-life insurance." ASTIN Bulletin 236 01 (1993): 95–115.
• Report on Non-Life Reserving Practices, from the ASTIN Working Party, IAA—June 2016.